Derivatives drawing
Table of Contents
Table of Contents
If you’re looking to take your calculus game to the next level, then learning how to draw derivative of a function is an essential skill. Sure, it might sound intimidating at first, but trust us: with a little bit of practice and guidance, you’ll be graphing those derivatives like a pro before you know it.
The Pain Points of Drawing Derivatives
One of the biggest pain points that people encounter when it comes to drawing derivatives is just understanding what they are and how they work. Specifically, it can be challenging to wrap your head around the idea that a derivative is essentially just a slope, but for a much smaller interval than what you’re used to dealing with when graphing linear functions.
Understanding How to Draw Derivatives
At its most basic level, knowing how to draw a derivative of a function simply comes down to finding the slope of that function at any given point. There are a few different ways that you can go about doing this, but one of the most straightforward methods involves using calculus and finding the limit of the average rate of change as Δx approaches 0.
Once you’ve found the derivative (i.e., the slope) at any given point, it’s just a matter of graphing that slope on a coordinate plane. You can do this by using the point-slope equation of a line or by simply plotting a point at the position of the derivative and “connecting the dots” to get a rough idea of what the curve should look like.
Main Points on Drawing Derivatives
So in summary, when it comes to drawing derivatives, you’ll want to:
- Understand what a derivative is (i.e., a slope at a specific point)
- Find the derivative using calculus
- Graph the derivative on a coordinate plane
My Personal Experience Learning to Draw Derivatives
When I first started learning how to draw derivatives, I have to admit that I was a bit intimidated by the whole process. Calculus had always been one of my weaker subjects, and the idea of graphing a “squiggly” line like a derivative seemed almost impossible.
But with the help of some patient teachers and some diligent practice, I slowly started to get the hang of it. I found that using calculus to find the derivative made a lot more sense once I started to see how the pieces fit together, and graphing the derivative itself became much easier once I realized that I was simply dealing with a bunch of tiny slopes instead of one big one.
Going Deeper into Drawing Derivatives
One of the trickier things about graphing derivatives is that they can look very different from the actual function that they’re derived from. For example, a function might have a sharp corner or a cusp, but the derivative at that point might still be perfectly smooth and continuous.
It’s also worth noting that there are a few different types of derivatives that you might encounter depending on the type of function you’re dealing with. For example, you might have to find the first derivative (i.e., the slope), second derivative (i.e., the rate of change of the slope), or even higher-order derivatives.
Tips for Perfecting Your Derivative-Drawing Skills
If you’re looking to become a true master of drawing derivatives, there are a few things that you can do to take your skills to the next level:
- Practice, practice, practice! There’s really no substitute for putting in the time and effort to get better at this skill.
- Work on your calculus skills. Understanding how to find the derivative is the first step towards being able to graph it accurately.
- Look for real-world examples to help solidify your understanding. For example, you might try graphing the derivative of a car’s position over time to see how the acceleration changes throughout the trip.
Common Questions About Drawing Derivatives
Q: Why are derivatives important in calculus?
A: Derivatives are one of the most fundamental concepts in calculus, and they’re used to solve a wide variety of problems. For example, they can help you find the maximum or minimum value of a function, determine the rate of change at any given point, or even help you calculate the area under a curve.
Q: What’s the difference between finding the derivative and graphing the derivative?
A: Finding the derivative involves using calculus to determine the slope of a function at any given point, while graphing the derivative involves using that slope to create a new curve that represents the rate of change of the original function.
Q: Can you graph a derivative without using calculus?
A: Technically speaking, yes, you could graph a derivative without using calculus, but it would be much more challenging. Calculus provides a relatively straightforward method for finding the slope of a curve at any given point, which makes graphing the derivative much easier than it would be otherwise.
Q: What’s the best way to check your work when graphing a derivative?
A: One of the easiest ways to check your work is simply to compare your graph to the original function that the derivative was derived from. If you’ve done everything correctly, the derivative should be an accurate representation of the way that the original function’s slope changes at any given point.
Conclusion of How to Draw Derivative of a Function
Drawing derivatives may seem daunting at first, but with a bit of practice and patience, anyone can learn how to do it. By following the steps outlined above, you’ll be well on your way to mastering this essential calculus skill and taking your math abilities to the next level.
Gallery
MATH221 Lesson 009B - Drawing Derivatives - YouTube

Photo Credit by: bing.com / derivatives drawing
Derivative Graph Vs Original Function (w/ 15+ Examples!)
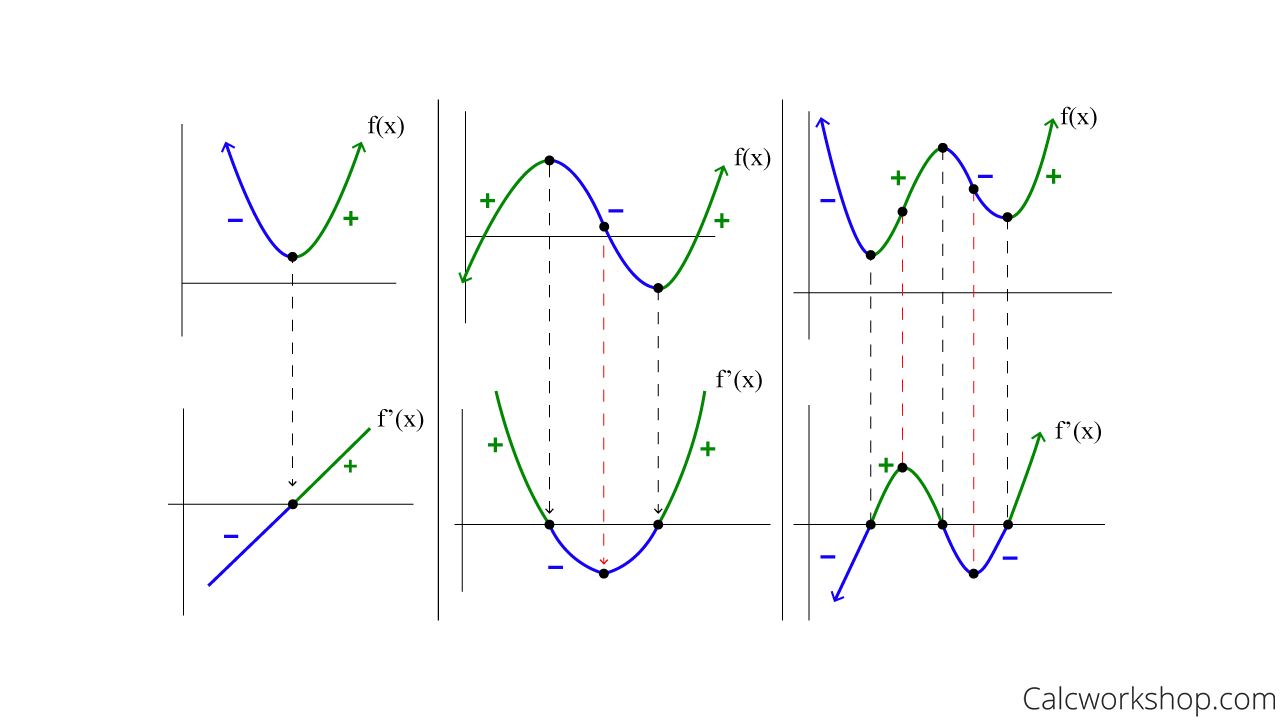
Photo Credit by: bing.com / derivative
Sketching The Derivative Of A Function | Doovi

Photo Credit by: bing.com / derivative function sketching
Draw The Function Given Graph Of Derivative - YouTube

Photo Credit by: bing.com / derivative graph function draw given
Sketching Derivative Graphs At PaintingValley.com | Explore Collection
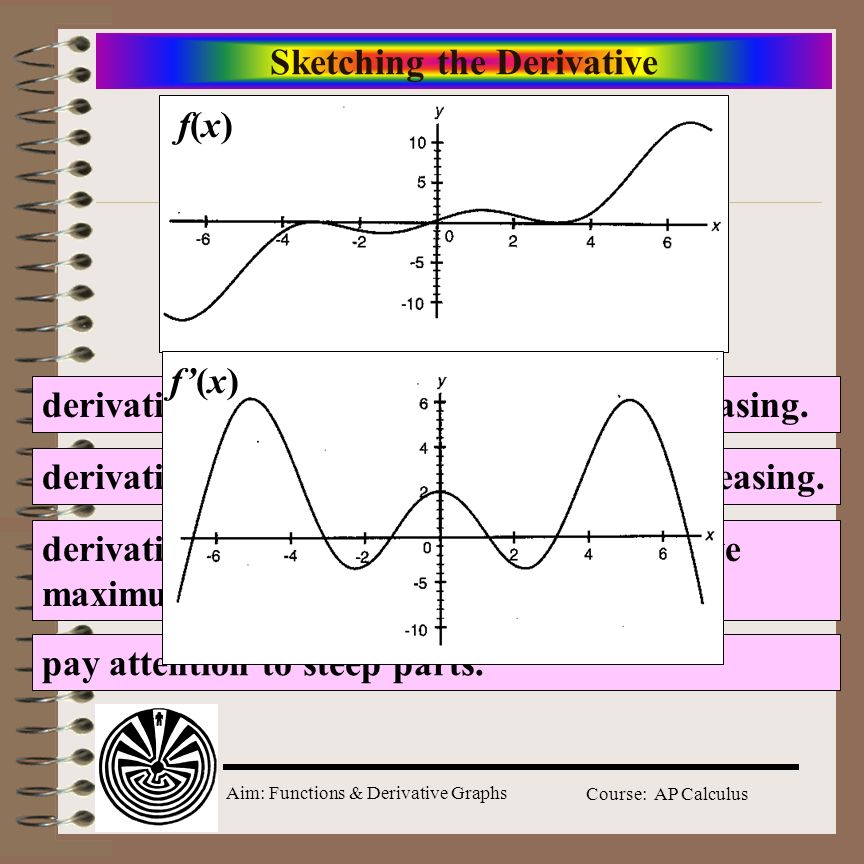
Photo Credit by: bing.com /