Histogram buckets bins construct grouped
Table of Contents
Table of Contents
Are you looking to create a histogram for ungrouped data but don’t know where to start? Histograms are an essential tool for analyzing data, and they can be useful in identifying patterns and trends. Creating a histogram for ungrouped data may seem intimidating at first, but with the right steps, it can be a straightforward process.
Pain Points of Drawing Histogram for Ungrouped Data
Not knowing how to organize and represent data is a common issue among beginners. Additionally, selecting the appropriate number of intervals, understanding how to set up an appropriate scale, and selecting a bin width that eliminates over-fitted or under-fitted curves can be other challenges.
How to Draw Histogram for Ungrouped Data
The first step to creating a histogram for ungrouped data is to determine the range of the data. Once you have determined the range, you can then calculate the bin width by dividing the range by the number of intervals you want to include. Then, using the bin width, establish the intervals for the histogram. Once these are established, draw the bars for each interval, with the height of each bar being proportional to the number of data points in that interval.
Summary of How to Draw Histogram for Ungrouped Data
To summarize, to draw a histogram for ungrouped data, you must first determine the range, calculate the bin width, establish the intervals for the histogram, and draw the bars for each interval. Properly organizing and representing data with histograms requires careful planning to determine the best bin width, and the proper scale selection, thus avoiding the under-fitted or over-fitted curves.
Choosing the Right Bin Width and Scale
The bin width affects how many bars the histogram will have and where the final bell or curve will be placed. A simple way of determining the most appropriate bin width for your data is using a square root formula. The formula involves taking the square root of the total number of data points and then rounding up to the next whole number. The output of this formula is a suggestion value for the number of bins, which should be adjusted to achieve the desired distribution shape. Choosing an appropriate scale to represent the data is also vital in the creation of a histogram.
Drawing the Bell Curve
To obtain the bell curve, make use of the data’s mean and standard deviations values, including the empirical rule or the normal distribution curve. The curve is symmetrical, mirroring the mean value with central tendencies at the peak of the curve. Its height represents the frequency of occurrence of the data.
Manipulating the Histogram
If you would like to reduce the range or scope of the histogram, you can crop the chart, thereby adjusting the scale to focus on the area of interest. You can also adjust the chart’s appearance by formatting the color, font, and additional design options on the chart.
Personal Experience of Drawing Histogram for Ungrouped Data
When I was first learning to draw a histogram, what initially stumped me was choosing the appropriate bin width. I would either have too few intervals, which would leave some data unaccounted for, or too many, which would create multiple peaks and an unappealing visual look. However, once I learned about the square root formula, it became much easier to determine the number of bins required, making the process more efficient and reliable.
Tips for Drawing a Histogram for Ungrouped Data
When deciding the bin width and the number of intervals, make sure to avoid selecting very small bin widths or too few intervals which will lead to an oversimplified histogram. Additionally, ensure that the height of each bar corresponds to the frequency or number of data points for that interval.
Question and Answer
Q: Why is it essential to calculate the number of intervals?
A: Calculating the number of intervals helps determine the bin width and the spread of data points between intervals, thereby allowing you to create a well-distributed histogram.
Q: What is an over-fitted histogram?
A: An over-fitted histogram is where the number of intervals is far too excessive, leading to each data point being isolated in its interval. The histogram doesn’t resemble a smooth curve, resulting in over-fitting of data.
Q: Do I need to scale the x-axis or y-axis when drawing a histogram?
A: Scaling the y-axis is vital since it represents the frequency of data occurrences in each interval. The x-axis only needs to show the intervals, and it does not need a scale since the intervals’ choice depends on the number of occurrences of data point in the data set.
Q: Is it possible to change the histogram’s design once it’s drawn?
A: Yes. You can manipulate and adjust the chart’s design by formatting color, font, and additional design options on the chart. You can also crop the chart to adjust the range being displayed.
Conclusion of How to Draw Histogram for Ungrouped Data
Drawing a histogram for ungrouped data is a critical step in understanding the distribution of the data. Choosing the bin width, the number of intervals, and the scale to represent the data is essential to produce a well-distributed histogram. With these tips and formulas, drawing a histogram for ungrouped data can be a smooth and efficient process.
Gallery
How To Make A Histogram : Bins Are The Buckets That Your Histogram Will
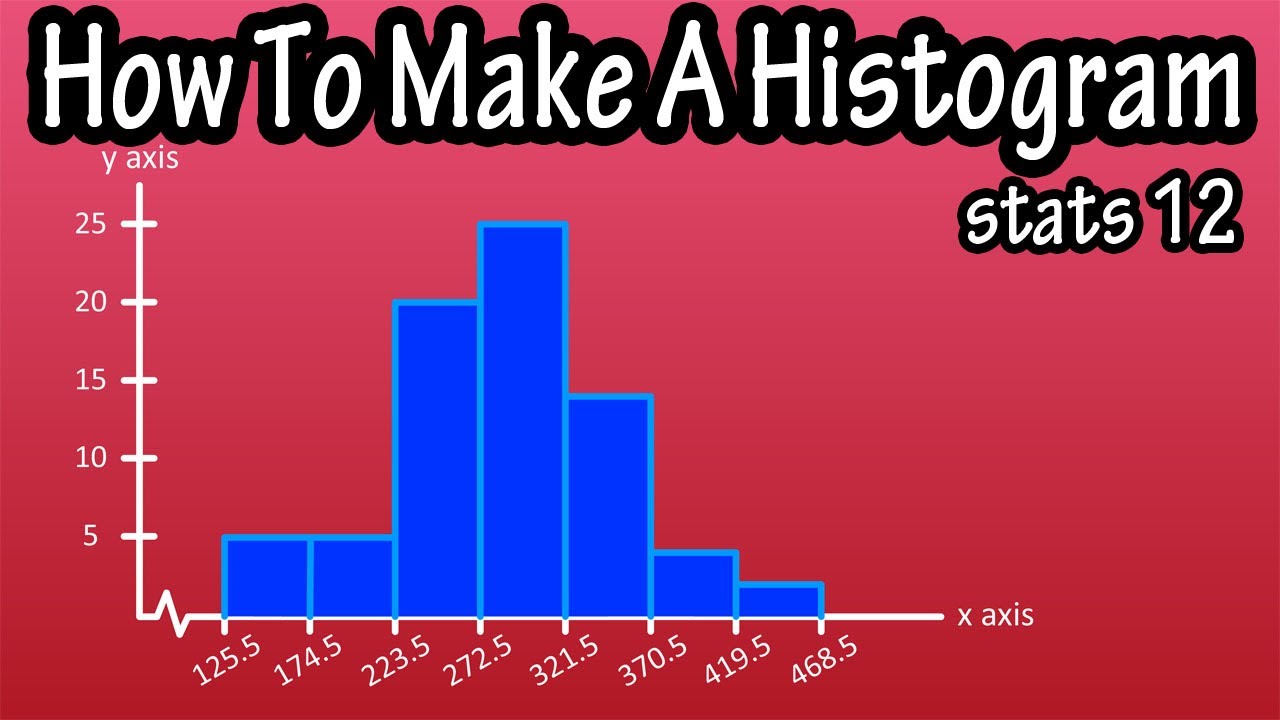
Photo Credit by: bing.com / histogram buckets bins construct grouped
How To Draw A Histogram
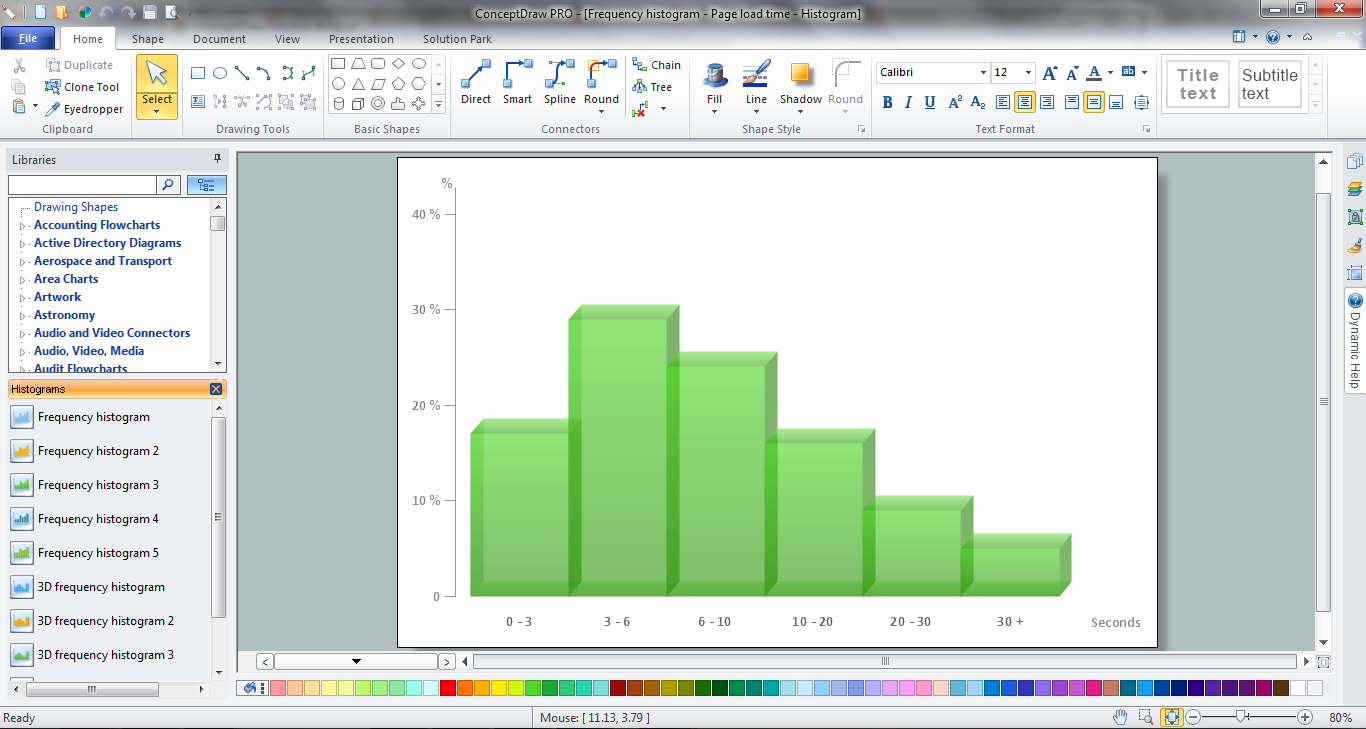
Photo Credit by: bing.com / histogram draw conceptdraw histograms diagram graph bar software pro example v12 guide graphs drawing chart
How To Make A Histogram - With Examples - Teachoo - Types Of Graph

Photo Credit by: bing.com / histogram
How To Explain Histogram - Histograms | DMAICTools.com - Such

Photo Credit by: bing.com / histogram histograms dataanalytics persistent inclusion quite stripchart
How To Draw A Histogram With Data

Photo Credit by: bing.com / histogram






